[Temporal Textures] Terry Tao: flows on Riemannian manifolds

Adrian, Andy, Michael, Tyr, Sean,

Another wrinkle for our scientific research agenda discussion (at 2 today) paralleling the discussions of "temporal textures"

Terry Tao is one of the most lucid communicative mathematicians of his generation. A key point for our purposes, I think, is the more general set up in which, instead of varying a metric g{t} with respect to the parameter "t" (putative time), one varies the base manifold as well. M becomes M(t). So a flow on a Riemannian manifold becomes a flow on a differentiable family of Riemannian manifolds:

Download PastedGraphic-3.pdf

Of course all the technical difficulty is in exactly how to vary through a family of manifolds, with potentially even changing topology. Tao treats the RIcci flow, which has become a pillar of mathematics in the past 20 years, including Perelman's settling of the Poincare Conjecture.

But in the spirit of a "small mammals in the age of large reptiles" strategy*, let me suggest a reversal of point of view, and read time from the evolutionary process. I draw attention to two points that Tao makes in the passage quoted below.

We enrich the notion of time by the notion of the flow of time itself, modelled by the "time vector field"

(1) The manifold developing topology goes hand in hand with the time vector field developing singularities. Think of chocolate flowing down a donut held vertically.

(2) The "time vector field $\partial_t \in \Gamma(T {\bf M})$ which obeys the transversality condition $\partial_t t = 1$ " gives a more precise generalization of the "directionality" of time, but this is only the beginning of the journey...

I would like to see if this can be illuminated by Adrian's discussion of lensing.

Xin Wei

(* Mammals and reptiles do not refer to mathematicians but to the unnamed ;)

http://terrytao.wordpress.com/2008/03/28/285g-lecture-1-ricci-flow/

"The one drawback of the above simple approach is that it forces the topology of the underlying manifold M to stay constant. A more general approach is to view each d-dimensional manifold M(t) as a slice of a d+1-dimensional “spacetime” manifold 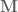${\bf M}$ (possibly with boundary or singularities). This spacetime is (usually) equipped with a time coordinate $t: {\bf M} \to {\Bbb R}$ , as well as a time vector field $\partial_t \in \Gamma(T {\bf M})$ which obeys the transversality condition $\partial_t t = 1$ . The level sets of the time coordinate t then determine the sets M(t), which (assuming non-degeneracy of t) are smooth d-dimensional manifolds which collectively have a tangent bundle $\hbox{ker}(dt) \subset T{\bf M}$ which is a d-dimensional subbundle of the d+1-dimensional tangent bundle $T{\bf M}$ of ${\bf M}$ . 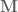The metrics g(t) can then be viewed collectively as a section ${\bf g}$ of $(\hbox{ker}(dt)^*)^{\otimes 2}$ . The analogue of the time derivative $\frac{d}{dt} g(t)$ is then the Lie derivative ${\mathcal L}_{\partial_t} {\bf g}$ . One can then define other Riemannian structures (e.g. Levi-Civita connections, curvatures, etc.) and differentiate those in a similar manner.

The former approach is of course a special case of the latter, in which ${\bf M} = M \times I$ for some time interval $I \subset {\Bbb R}$ with the obvious time coordinate and time vector field. The advantage of the latter approach is that it can be extended (with some technicalities) into situations in which the topology changes (though this may cause the time coordinate to become degenerate at some point, thus forcing the time vector field to develop a singularity). This leads to concepts such as generalised Ricci flow, which we will not discuss here, though it is an important part of the definition of Ricci flow with surgery (see Chapters 3.8 and 14 of Morgan-Tian’s book for details)."